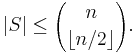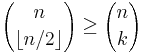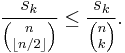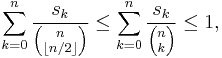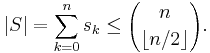Sperner family

In combinatorics, a Sperner family (or Sperner system), named in honor of Emanuel Sperner, is a set system (F, E) in which no element is contained in another. Formally,

If X, Y are in F and X ≠ Y, then X is not contained in Y and Y is not contained in X.

Equivalently, a Sperner family is an antichain in the inclusion lattice over the power set of E. A Sperner family is also sometimes called an independent system or, if viewed from the hypergraph perspective, a clutter.

1 Dedekind numbers
2 Sperner's theorem
- 2.1 Proof
3 Clutters
- 3.1 Examples
- 3.2 Minors
4 References
5 External links

Dedekind numbers

Main article: Dedekind number

The number of different Sperner families on a set of n elements is counted by the Dedekind numbers, the first few of which are

2, 3, 6, 20, 168, 7581, 7828354, 2414682040998, 56130437228687557907788 (sequence A000372 in OEIS).

Although accurate asymptotic estimates are known for larger values of n, it is unknown whether there exists an exact formula that can be used to compute these numbers efficiently.

Sperner's theorem

The k-subsets of an n-set form a Sperner family, the size of which is maximized when k = n/2. Sperner's theorem (a special case of Dilworth's theorem) states that these families are the largest possible Sperner families over an n-set. Formally, the theorem states that, for every Sperner family S over an n-set,

$|S| \le {n \choose \lfloor{n/2}\rfloor}.$

It is sometimes called Sperner's lemma, but that name also refers to another result on coloring. To differentiate the two results, the result on the size of a Sperner family is now more commonly known as Sperner's theorem.

A graded partially ordered set is said to have the Sperner property when one of its largest antichains is formed by a set of elements that all have the same rank; Sperner's theorem states that the poset of all subsets of a finite set, partially ordered by set inclusion, has the Sperner property.

Proof

The following proof is due to Lubell (see reference). Let s_k denote the number of k-sets in S. For all 0 ≤ k ≤ n,

${n \choose \lfloor{n/2}\rfloor} \ge {n \choose k}$

and, thus,

${s_k \over {n \choose \lfloor{n/2}\rfloor}} \le {s_k \over {n \choose k}}.$

Since S is an antichain, we can sum over the above inequality from k = 0 to n and then apply the LYM inequality to obtain

$\sum_{k=0}^n{s_k \over {n \choose \lfloor{n/2}\rfloor}} \le \sum_{k=0}^n{s_k \over {n \choose k}} \le 1,$

which means

$|S| = \sum_{k=0}^n s_k \le {n \choose \lfloor{n/2}\rfloor}.$

This completes the proof.

Clutters

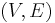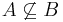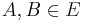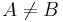A clutter H is a hypergraph $(V,E)$ , with the added property that $A \not\subseteq B$ whenever $A,B \in E$ and $A \neq B$ (i.e. no edge properly contains another). That is, the sets of vertices represented by the hyperedges form a Sperner family. Clutters are an important structure in the study of combinatorial optimization. The opposite notion of a clutter is an abstract simplicial complex, where every subset of an edge is contained in the hypergraph.

If 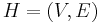$H = (V,E)$ is a clutter, then the blocker of H, denoted 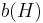$b(H)$ , is the clutter with vertex set V and edge set consisting of all minimal sets 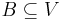$B \subseteq V$ so that 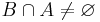$B \cap A \neq \varnothing$ for every 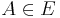$A \in E$ . It can be shown that 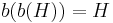$b(b(H)) = H$ (Edmonds & Fulkerson 1970), so blockers give us a type of duality. We define 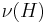$\nu(H)$ to be the size of the largest collection of disjoint edges in H and 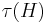$\tau(H)$ to be the size of the smallest edge in 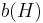$b(H)$ . 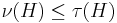It is easy to see that $\nu(H) \le \tau(H)$ .

Examples

If G is a simple loopless graph, then 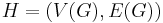$H = (V(G),E(G))$ is a clutter and 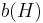$b(H)$ is the collection of all minimal vertex covers. Here 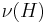$\nu(H)$ is the size of the largest matching and 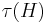$\tau(H)$ is the size of the smallest vertex cover. König's theorem states that, for bipartite graphs, $\nu(H) = \tau(H)$ . However for other graphs these two quantities may differ.
Let G be a graph and let 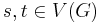$s,t \in V(G)$ . Define 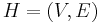$H = (V,E)$ by setting 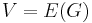$V = E(G)$ and letting E be the collection of all edge-sets of s-t paths. Then H is a clutter, and 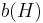$b(H)$ is the collection of all minimal edge cuts which separate s and t. In this case 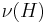$\nu(H)$ is the maximum number of edge-disjoint s-t paths, and 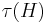$\tau(H)$ is the size of the smallest edge-cut separating s and t, so Menger's theorem (edge-connectivity version) asserts that $\nu(H) = \tau(H)$ .
Let G be a connected graph and let H be the clutter on 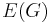$E(G)$ consisting of all edge sets of spanning trees of G. Then 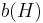$b(H)$ is the collection of all minimal edge cuts in G.

Minors

There is a minor relation on clutters which is similar to the minor relation on graphs. If 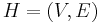$H = (V,E)$ is a clutter and 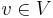$v \in V$ , then we may delete v to get the clutter 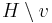$H \setminus v$ with vertex set 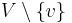$V \setminus \{v\}$ and edge set consisting of all 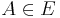$A \in E$ which do not contain v. We contract v to get the clutter 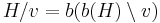$H / v = b(b(H) \setminus v)$ . These two operations commute, and if J is another clutter, we say that J is a minor of H if a clutter isomorphic to J may be obtained from H by a sequence of deletions and contractions.

References

Engel, K. (2001), "Sperner theorem", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1556080104, http://www.encyclopediaofmath.org/index.php?title=S/s130500
Anderson, Ian (1987), "1.2 Sperner's theorem", Combinatorics of Finite Sets, Oxford University Press, pp. 2–4 .
Knuth, Donald E. (2005), "Draft of Section 7.2.1.6: Generating All Trees", The Art of Computer Programming, IV, pp. 17–19, http://www-cs-faculty.stanford.edu/~knuth/fasc4a.ps.gz .
Lubell, D. (1966), "A short proof of Sperner's lemma", Journal of Combinatorial Theory 1 (2): 299, doi:10.1016/S0021-9800(66)80035-2, MR 0194348 .
Sperner, Emanuel (1928), "Ein Satz über Untermengen einer endlichen Menge" (in German), Mathematische Zeitschrift 27 (1): 544–548, doi:10.1007/BF01171114, JFM 54.0090.06 .
Edmonds, J.; Fulkerson, D. R. (1970), "Bottleneck extrema", Journal of Combinatorial Theory 8 (3): 299–306, doi:10.1016/S0021-9800(70)80083-7 .

External links

Sperner's Theorem at cut-the-knot
Sperner Theory by Konrad Engel.
Sperner's theorem on the polymath1 wiki